Glosario.

Unidad III

Glosario 

1)Punto: El Punto se define como un elemento geométrico que no tiene longitud, anchura, ni altura; se asemeja a la huella dejada por un alfiler. Este solo ocupa un lugar en el espacio.

• 

2) Linea: son en geometría un elemento de construcción de planos y figuras.

3) Line recta: Sucesión de infinitos puntos (no tiene principio ni fin, es decir no tiene límites) donde los puntos están alineados en una misma dirección.

 


4) Semirrecta: El concepto de semirrecta se utiliza en geometría para identificar a cada uno de los fragmentos en que toda recta puede ser dividida por cualquiera de los puntos que la componen.
 

5) Segmento de linea recta: Segmento de recta: si tomamos 2 puntos en una recta (T y S), el segmento de recta sera el conjunto de puntos comprendidos entre T y S.




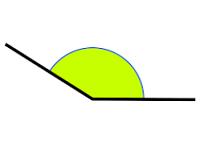
 6) Angulo: Se forma a partir de dos rectas que se cortan entre sí en una misma superficie.También puede decirse que un ángulo está formado por dos semirrectas que comparten un mismo vértice.











 7) Sistemas de medicion de angulos (grados(decimal y sexagecimal) radianes).

Los grados sexagesimal dividen una circunferencia en 360 partes iguales, de manera que una vuelta a la misma son 360º. 360º Su símbolo es °.












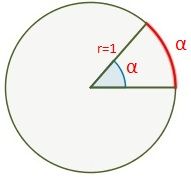
El radián es una unidad de medida del Sistema Internacional de Unidades. Es el ángulo de la circunferencia que abarca un arco de longitud igual al radio de la misma. Su símbolo es rad.













El "Grado" es la unidad empleada para clasificar los ángulos en las figuras geométricas (generalmente entre dos rectas o segmentos).

 

















Convertir de grados a radianes: Ver el siguiente video.

Convertir de grados decimal a sexagecimal: Ver el siguiente video.

8) Una clasificacion de angulos segun su medida es: Ver el siguiente video.

 9) Otra clasificacion de los angulos segun su posicion es:

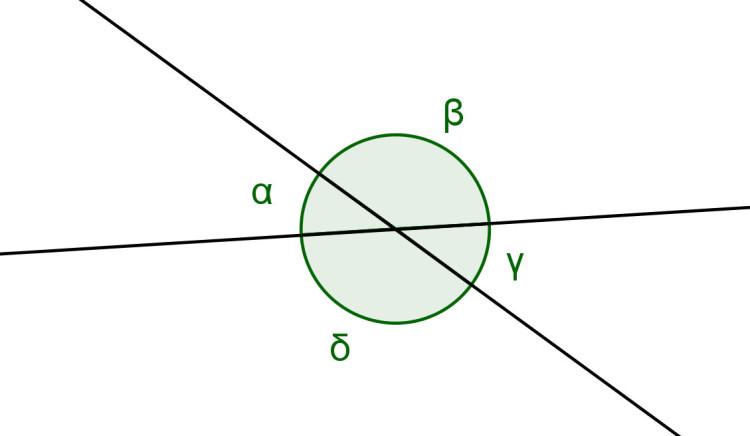
Ángulos adyacentes son aquellos que tienen el vértice y un lado común, y los otros lados situados uno en prolongación del otro. Forman un ángulo llano.
 
Ángulos opuestos por el vértice son los que teniendo el vértice común, los lados de uno son prolongación de los lados del otro.





 Los ángulos suplementarios son aquellos que en par suman 180 grados. A diferencia de los ángulos complementarios que forman 90 grados. Siguiendo la misma propiedad y fórmula de los que se complementan entre sí, un ángulo que tenga menos de 180 grados le corresponderá un ángulo que lo suplementa según la fórmula A (ángulo suplementario) = 180° menos (-) el ángulo que necesita suplemento. Ejemplo: A = 180° – 150° = 30°.





Los ángulos complementarios son los que sumados son iguales al valor de un ángulo recto, es decir, un ángulo de 90 grados.



10)Triangulo:
El triángulo es un polígono de tres lados que da origen a tres vértices y tres ángulos internos. Es la figura más simple, después de la recta en la geometría. Como norma general un triángulo se representa con tres letras mayúsculas de los vértices (ABC).



11) Clasificacion de los angulos segun sus lados.

1) triángulos equiláteros

Las palabras equi - látero vienen del latín: igual – lado.

Son los triángulos cuyos tres lados son iguales: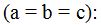 

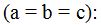
2) triángulos isósceles
La palabra isósceles está compuesta de dos palabras griegas isoque significa igual y de la palabra skeles que podemos traducir por piernas.

La palabra isósceles referido a la geometría quiere decir que dos lados (piernas) son iguales. Por lo tanto, un triángulo con dos lados iguales llamamos isósceles.

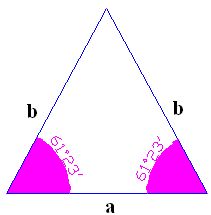
Como ves en la figura, tienes el triángulo isósceles con dos lados iguales. Si tiene 2 lados iguales tendrá también dos ángulos iguales.

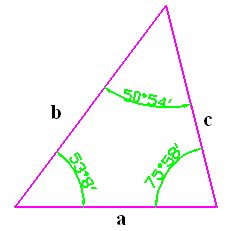
3) triángulos escalenos

La palabra escaleno procede de la palabra griega skaleno que significa cojear, cojo. Nos da la idea que si el triángulo “cojea” sus lados no son iguales. Efectivamente, el triángulo escaleno tiene sus lados diferentes por lo que sus ángulos también serán diferentes.

12) Clasificacion de los triangulos segun sus angulos:

1) Triángulos rectángulos si tienen UN ángulo recto.

Tienes a continuación tres ejemplos de triángulos rectángulos

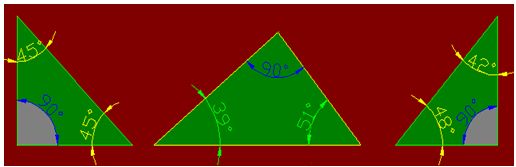
En un triángulo rectángulo, el lado opuesto al ángulo recto se llama hipotenusa y los lados perpendiculares que forman el ángulo recto se llaman catetos.

2) Triángulos acutángulos, si tienen TRES ángulos agudos(menores de 90º).

En el dibujo siguiente tienes dos triángulos acutángulos.

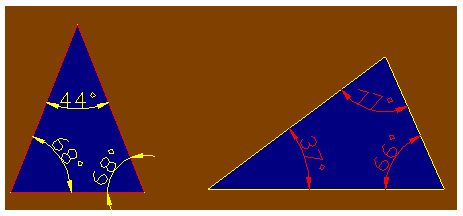
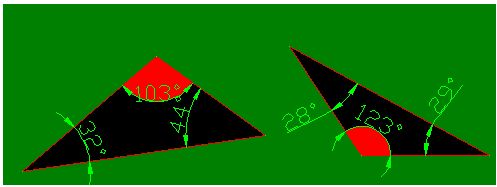
3) Triángulos obtusángulos, si tienen UN ángulo obtuso (más de 90º).

En la siguiente figura tienes dos triángulos obtusángulos

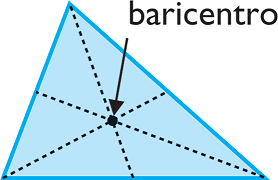
13) Rectas y puntos notables en el triángulo:
 La mediana es el segmento que va desde un vértice hasta el punto medio del lado opuesto. El punto de corte se llama Baricentro (centro de gravedad del triángulo)

 La mediatriz de un segmento es la perpendicular a dicho segmento por su punto medio. También es el lugar geométrico de los puntos que equidistan de los extremos del segmento. Su punto de corte se llama circuncentro (centro de la circunferencia circunscrita).

 La altura de un triángulo es la recta perpendicular a un lado (ó a su prolongación) por el vértice opuesto. El punto de corte de las alturas es el ortocentro.

 La bisectriz de un ángulo es la semirrecta que divide al ángulo en dos partes iguales. También es el lugar geométrico de los puntos que equidistan de los lados del ángulo. El punto de corte de las bisectrices es el incentro (centro de la circunferencia inscrita).














14) Poligonos regulares e irregulares.

Polígono Regular 

Polígono en el cual todos sus lados son de igual longitud, y todos sus vértices están circunscritos en una circunferencia.
 

Polígono Irregular 

Polígono en el cual sus lados no son de igual longitud y/o sus vértices no están contenidos  en una circunferencia. De acuerdo al número de sus lados, se denominan:

15) Propiedades de los poligonos:

a) Suma de sus angulos interiores.

La suma de los ángulos de un triángulos es 180°.
Es fácil ver que la suma de los ángulos interiores del polígono, es la suma de los ángulos de los triángulos.


b) Numero de triangulos que se forman en el interior:

1. Un polígono con n lados, tienen como suma de sus ángulos interiores 180° (n – 2)
Se toma como referencia un vértice cualquiera y se trazan (n – 2) triángulos en el polígono.
 

16)Perimetro y Area de poligonos:

El perímetro de un polígono es igual a la suma de las longitudes de sus lados y su área es la medida de la región o superficie encerrada por un polígono.
 

17) Formula de Heron:

La fórmula de Herón halla el área de un triángulo del cual se conocen todos sus lados. El área se calcula a partir del semiperímetro del triángulo s y de la longitud de los lados (a, b y c).




18) Circunferencia, rectas y segmentos en:

Circunferencia:

Es una línea curva cerrada y plana formada por un conjunto de puntos que equidistan de otro punto fijo llamado centro “O”, la distancia constante del centro a todos los puntos de la circunferencia recibe el nombre de radio.

También podemos definirá a la circunferencia como el contorno o perímetro del círculo.

PUNTOS, SEGMENTOS Y RECTAS DE LA CIRCUNFERENCIA

·      Centro, el punto interior equidistante de todos los puntos de la circunferencia.

·      Radio, el segmento que une el centro con un punto cualquiera de la circunferencia.

·      Diámetro, el mayor segmento que une dos puntos de la circunferencia y  que necesariamente pasa por el centro.

·      Cuerda, el segmento que une dos puntos de la circunferencia; (las cuerdas de longitud máxima son los diámetros).

·      Arco, el segmento curvilíneo de puntos pertenecientes a la circunferencia.

·     Semicircunferencia, cada uno de los dos arcos delimitados por los extremos de un diámetro.

19) Angulos en la circunferencia:

ÁNGULOS EN LA CIRCUNFERENCIA

·            Ángulo central tiene su vértice en el centro por lo que sus lados contienen a dos radios. La amplitud de un ángulo central es igual a la del arco que abarca.

·            Ángulo inscrito su vértice es un punto de la circunferencia y sus lados son dos cuerdas.

·            Ángulo semi-inscrito su vértice es un punto de la circunferencia y sus lados contienen una cuerda y una recta tangente a la circunferencia. El vértice es el punto de tangencia. La amplitud de un ángulo semi-inscrito es la mitad de la del arco que abarca.

·            Ángulo interior su vértice está en el interior de la circunferencia. La amplitud de un ángulo interior es la mitad de la suma de dos medidas: la del arco que abarcan sus lados más la del arco que abarcan sus prolongaciones.

·            Ángulo exterior tiene su vértice en el exterior de la circunferencia  y los lados de sus ángulos son: o secantes a ella, o uno tangente y otro secante, o tangentes a ella.

Fuentes bibliograficas:

http://solecito21roch.blogspot.mx
http://www.universoformulas.com/matematicas/geometria/formula-heron/
https://www.portaleducativo.net/octavo-basico
http://www.infoymate.es/mate/geomcuad/periarea/periarea.htm
https://es.slideshare.net/oscaritoinside/propiedades-de-los-poligonos
https://propiedadesdelospoligonos.mx
http://mateceblag2013.blogspot.mx/2012/11/poligonos-regulares-e-irregulares.html https://www.geogebra.org/m/NKCCWWDj
https://www.ecured.cu/Rectas_y_puntos_notables_de_un_tri%C3%A1ngulo
http://www.universoformulas.com/matematicas/geometria/triangulo/
www.aulafacil.com/cursos/l11143/ciencia/matematicas/geometria/

www.ConceptoDefinicion.de/linea

 https://www.smartick.es/blog/matematicas/geometria/lineas-rectas

https://geometriaeltrigo.wordpress.com/unidades

http://www.estudiantes.info/matematicas/1eso/images/puntos-y-rectas-desarrollo.html.